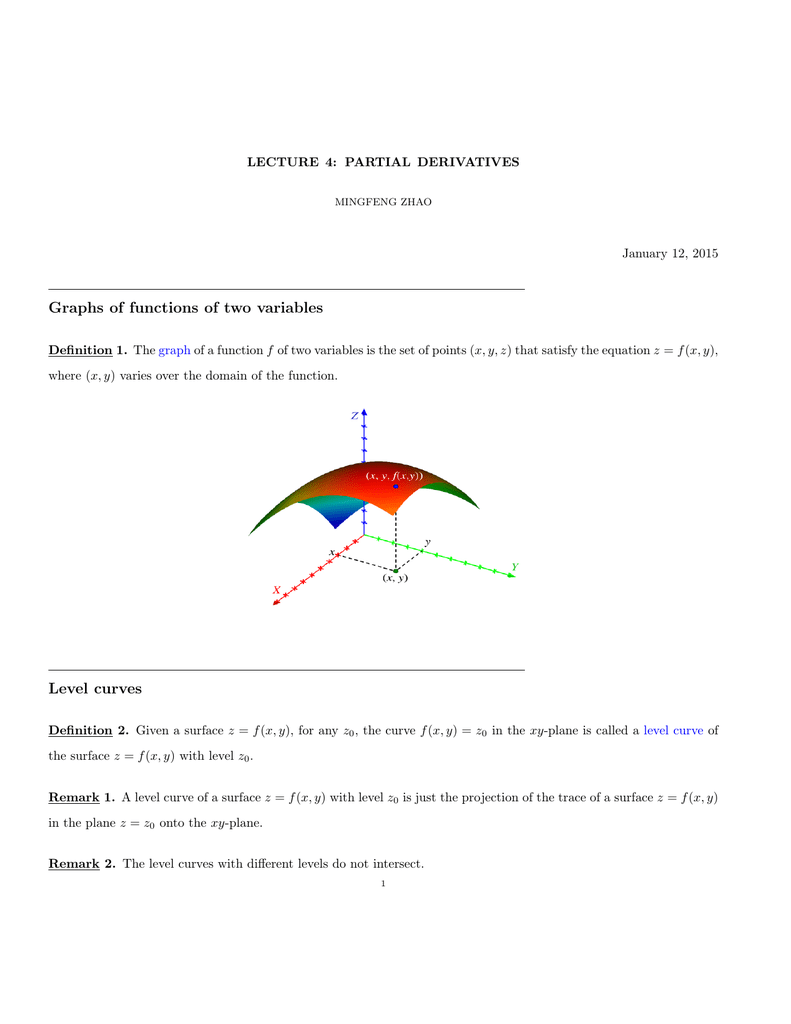
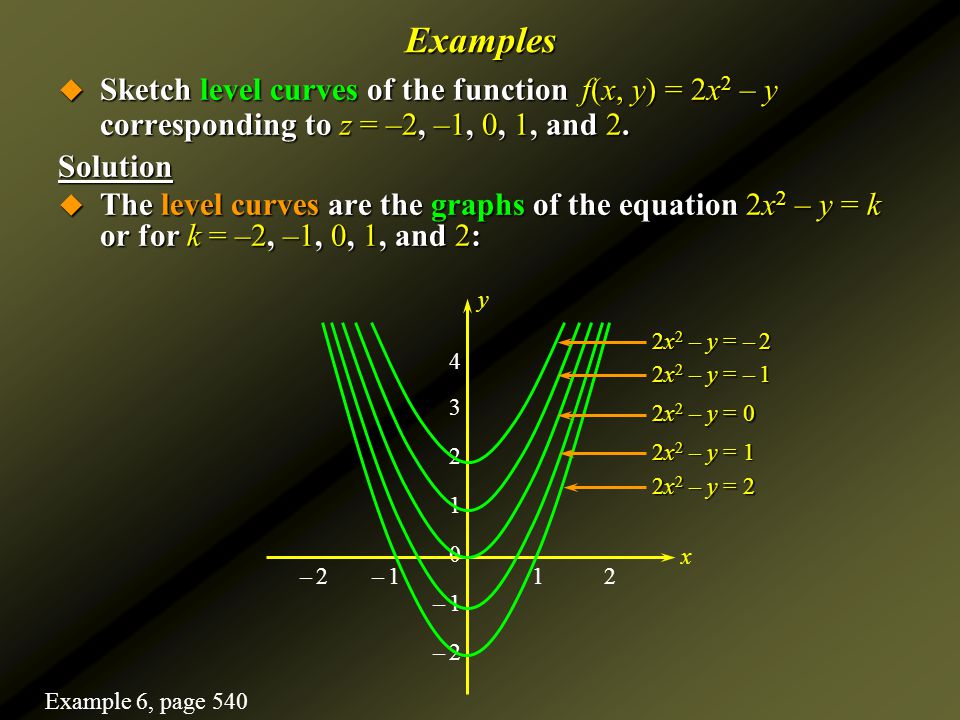
This video is a gentle introduction to functions of several variables We motivate the topic and show how to sketch simple surfaces associated with functionLevel Curves Def If f is a function of two variables with domain D, then the graph of f is {(x,y,z) ∈ R3 z = f(x,y) } for (x,y) ∈ D Def The level curves of a function f(x,y)are the curves in the plane with equations f(x,y)= kwhere is a constant in the range of f The contour curves are the corresponding curves on the surface, theOUTLINE • 11 Function of Two Variables • Graph of the Function in 3D Coordinate system • Some Common Surfaces • Trace (Sketch the trace) • Level Curve (Sketch the level curve) • 12 Function of Three Variables • Level Surface (Sketch the level surface) (x,y) (a, b) f (x,y) f (a,b) z = f (x,y) 11 Function of Two Variables Graph of the function Graph of z = f (x,y) is a set of

Level Curves
What are level curves of a function
What are level curves of a function-For a function of three variables, one technique we can use is to graph the level surfaces, our threedimensional analogs of level curves in two dimensions Given , the level surface at is the surface in space formed by all points where Section 15 Functions of Several Variables For problems 1 – 4 find the domain of the given function f (x,y) = √x2−2y f ( x, y) = x 2 − 2 y Solution f (x,y) = ln(2x −3y1) f ( x, y) = ln ( 2 x − 3 y 1) Solution f (x,y,z) = 1 x2 y2 4z f ( x, y, z) = 1 x 2 y 2 4 z Solution
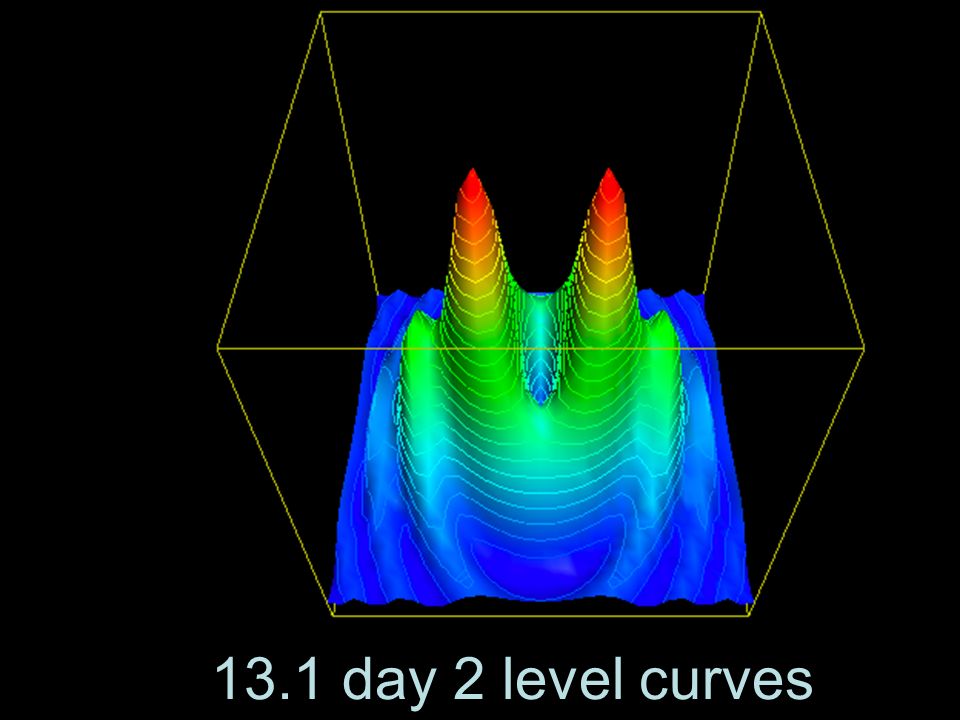



13 1 Day 2 Level Curves Level Curves One Way To Visualize A Function Of Two Variables Is To Use A Scalar Field In Which The Scalar Z F X Y Is Assigned
A function of two variables is a surface drawn in 3 dimensions;Level Curves and Contour Maps The level curves of a function f(x;y) of two variables are the curves with equations f(x;y) = k, where kis a constant (in the range of f) A graph consisting of several level curves is called a contour map Level Surfaces The level surfaces of a function f(x;y;z) of three variables are the surfacesX y 143 Level Curves and Level Surfaces Look over book examples!!!
The syntax of the command is the threevariable version of the syntax of the ContourPlot command to generate the level curves of a function of two variables ContourPlot3DFx, y, z, {x, xmin, xmax}, {y, ymin, ymax}, {z, zmin, zmax} A function of one variable is a curve drawn in 2 dimensions;MATH 1 Multivariable Calculus at Queens College, Spring 21
Transcribed image text CURRENT OBJECTIVE Find the level curves of a function of two variables Question Choose the most specific description for the level curve of the function g(1,y) = zhy corresponding to c= 2 Select the correct answer below a line passing through the origin, excluding the origin a line passing through the origin O parabola ellipse(a) The level curves of a function of two variables are specified as f(x,y) =const Express the derivative of this function at any point (x,y) in terms of the partial derivatives of f(x,y) Draw some level curves of the real and imaginary parts of the function w = z'in the (x,y) planeFunctions of 2 Variables, Graphs, Level Curves Functions of 3 Variables, Level Surfaces Calculus of Multivariable Functions, Limits, TwoPath Test Week 5 Sec Partial First and Higher Order Derivatives, Clairaut Theorem, Differentiability Chain Rule, Implicit Differentiation Gradient, Directional Derivative Week 6



Level Curves Functions Of Several Variables By Openstax Page 3 12 Jobilize




Sketch Saddle Point Of A Function Of Two Variables F X Y 4 X 3 Y 3 3xy Stewart P930 Question 14 7 3 Mathematics Stack Exchange
Level sets show up in many applications, often under different names For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implicit equationAnalogously, a level surface is sometimes called an implicit surface or an isosurface The name isocontour is also used, which means a contour of(3 points) Writing Prompt (typed 1000 words) In your own words, define the level curves of a function of two variables Describe how level curves can help you sketch a graph of a surface Give examples of several surfaces whose level curves are circles and at least one example of a surface whose level curves are not circlesExamples of level curves for different types of functions example of limits in multivariable calculus one exists and one doesn't exist;




Level Set Wikipedia




13 1 Day 2 Level Curves Level Curves One Way To Visualize A Function Of Two Variables Is To Use A Scalar Field In Which The Scalar Z F X Y Is Assigned
A level curve (or contour) of a function \(f\) of two independent variables \(x\) and \(y\) is a curve of the form \(k = f(x, y)\), where \(k\) is a constant Topographical maps can be used to create a threedimensional surface from the twodimensional contours or level curvesLevel curves and contour plots are another way of visualizing functions of two variables If you have seen a topographic map then you have seen a contour plot Example To illustrate this we first draw the graph of z = x2 y2 On this graph we draw contours, which are curves at a fixed height z = constant For example the curve at height zCalculus 3 Lecture 131 Intro to Multivariable Functions (Domain, Sketching, Level Curves) Working with Multivariable Functions with an emphasis on findi




Functions Of Two And Three Variables Level Curves Contours Level Surfaces Youtube




14 Partial Derivatives Partial Derivatives So Far We
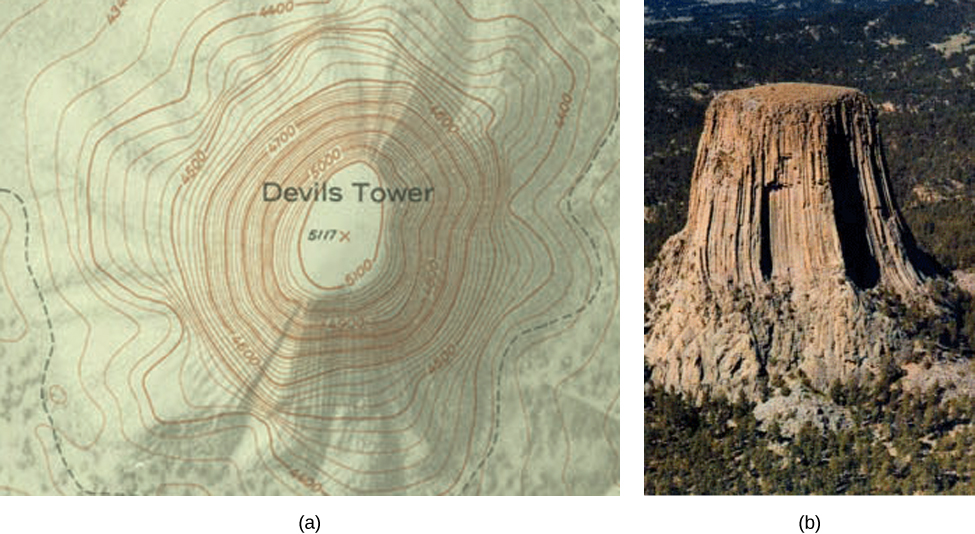
A level curve of a function of two variables is completely analogous to a contour line on a topographical map (a) A topographical map of Devil's Tower, Wyoming Lines that are close together indicate very steep terrainLevel Curves and Surfaces Example 2 In mathematics, a level set of a function f is a set of points whose images under f form a level surface, ie a surface such that every tangent plane to the surface at a point of the set is parallel to the level setSay for example I give you a function of two variables z = f (x, y) = x 2 y 2 which represents a paraboloid If I want the level curves f (x, y) = c, then these now represent concentric circles in the x − y plane centered at the origin of radius c Now here's my question
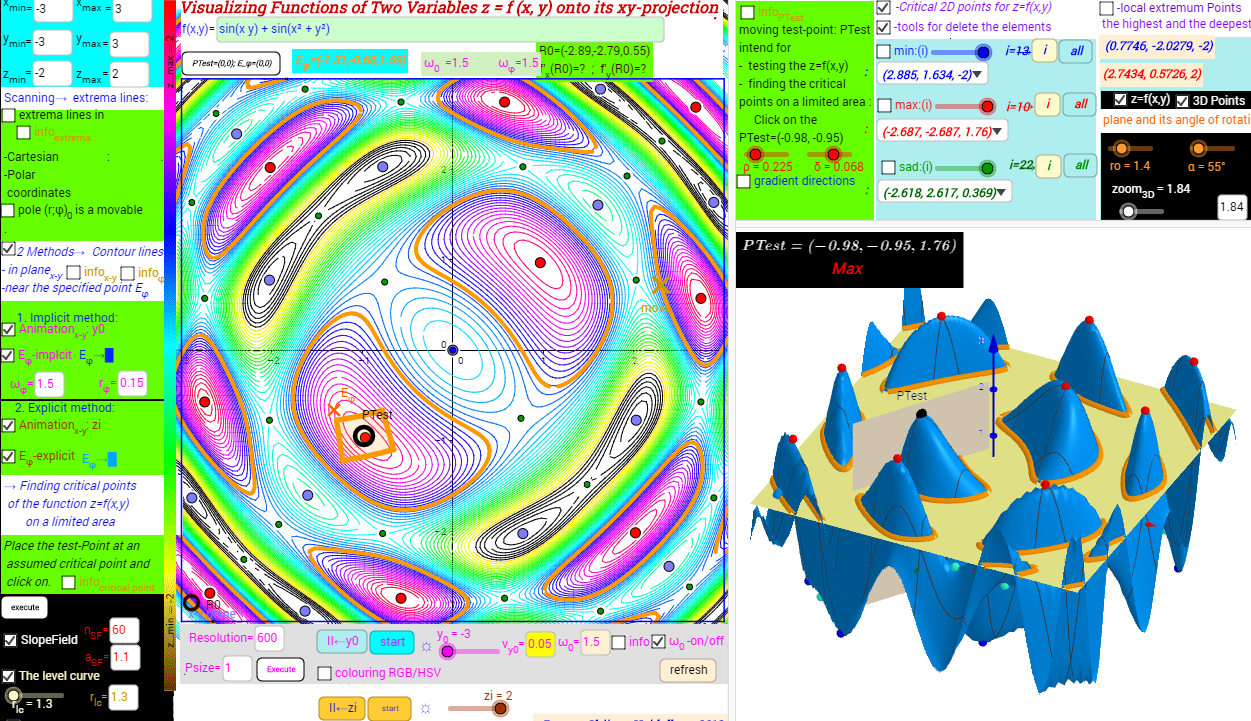



Sin X Y Sin X 2 Y 2 Images To Visualizing Functions Of Two Variables Geogebra
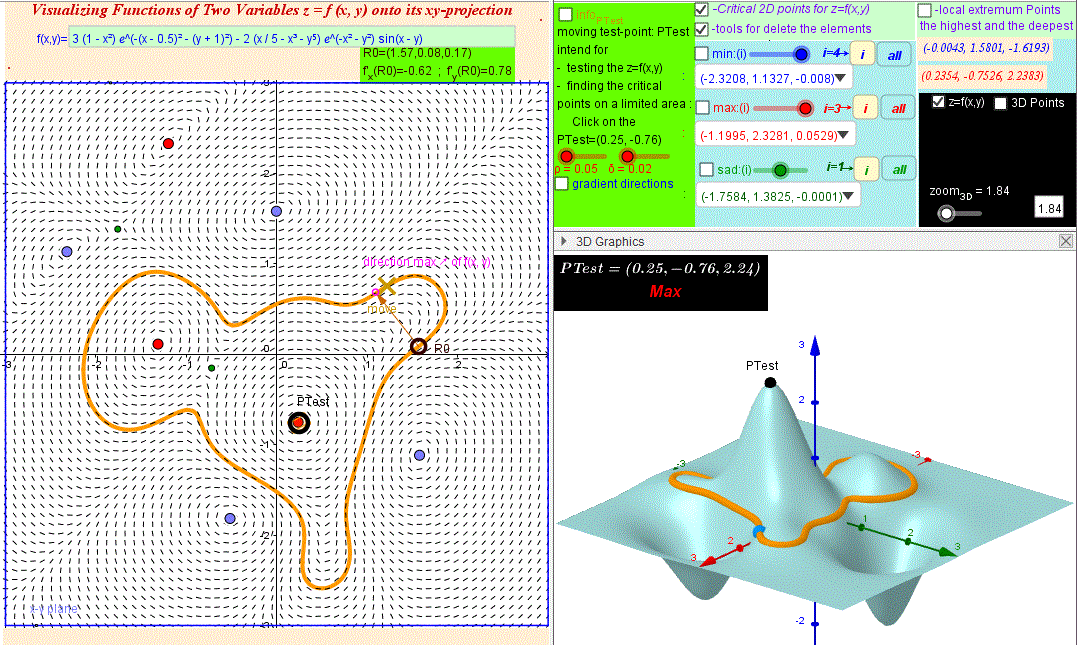



Visualizing Functions Of Two Variables Geogebra
2 Function of two variables For function z = f(x;y) We can talk about the tangent plane of the graph, the normal line of the tangent plane(or the graph), the tangent line of the level curve, the normal line of the level curve Tangent plane and the normal line of the graph are in xyz space while the things related to level curve are in xy planeA level curve of a function of two variables f (x, y) f (x, y) is completely analogous to a contour line on a topographical map Figure 47 (a) A topographical map of Devil's Tower, Wyoming Lines that are close together indicate very steep terrain (b) A perspective photo of Devil's Tower shows just how steep its sides areExample of when a limit does not exist for a function of two variables 1




Ppt Chapter 14 Partial Derivatives Powerpoint Presentation Free Download Id



Non Convex Level Curves And Their Corresponding Pairs Of Download Scientific Diagram
One way to collapse the graph of a scalarvalued function of two variables into a twodimensional plot is through level curves A level curve of a function f (x, y) is the curve of points (x, y) where f (x, y) is some constant value A level curve is simply a cross section of the graph of z = f (x, y) taken at a constant value, say z = cMy Partial Derivatives course https//wwwkristakingmathcom/partialderivativescourseIn this video we're talking about how to sketch the level curves of Determine the directional derivative in a given direction for a function of two variables Determine the gradient vector of a given realvalued function Explain the significance of the gradient vector with regard to direction of change along a surface Use the gradient to find the tangent to a level curve of a given function




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




14 Partial Derivatives Copyright Cengage Learning All Rights
The domain, range, and graph of z=f(x,y) The definitions and notation used for functions with two variables are similar to those for one variableThe remaining arguments are optional The next one specifies the particular MATLAB plotting function that will be used The defaults are 'plot' for functions of one variable or two component parametrized curves, 'plot3' for three dimensional parametrized curves, and 'surf' for functions of two variables or parametrized surfacesGiven a functionf(x, y), the setf(x, y) =c= const is called acontour curveorlevel curve off For example, forf(x, y) = 4x2 3y2the level curvesf=care ellipses ifc >0 Level curves allow to visualize functions of two variablesf(x, y) ExampleForf(x, y) =x2−y2




Level Curves Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



12 1 Introduction To Multivariable Functions Mathematics Libretexts
Definition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f ) A level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f has height kFor a function of three variables f (x,y,z) the notion corresponding to the level curve of a twovariable function is a level surface, f (x,y,z)=c This is generally a surface, which can be plotted with the help of MapleLevel Surfaces It is very difficult to produce a meaningful graph of a function of three variables A function of one variable is a curve drawn in 2 dimensions;




11 Level Curves And Contour Lines Of Functions Of Two Variables Youtube



1
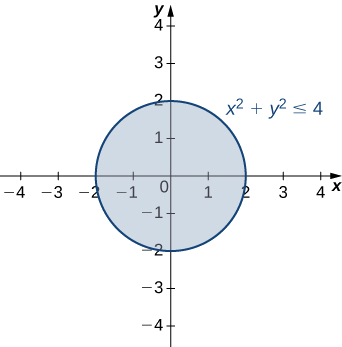
Just as the graph of a function f of one variable is a curve Cwith equation y = f (x), so the graph of a function f of twovariables is a surface S with equation z = f (x, y)We can visualize the graph S of f as lying directly above orbelow its domain D in the xyplane (see Figure 5) Figure 5When we talk about the graph of a function with two variables defined on a subset D of the xyplane, we mean zfxy xy D= (, ) ,( )∈ If c is a value in the range of f then we can sketch the curve f(x,y) = cThis is called a level curve A collection of level curves can give a good representation of the 3d graph Given a function f(x, y) and a number c in the range of f, a level curve of a function of two variables for the value c is defined to be the set of points satisfying the equation f(x, y) = c Returning to the function g(x, y) = √9 − x2 − y2, we can determine the level curves of this function The range of g is the closed interval 0, 3



1



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework13 1 Ans Pdf
A function of three variables is a hypersurface drawn in 4 dimensions» Clip Level Curves and Contour Plots () From Lecture 8 of 1802 Multivariable Calculus, Fall 07 Flash and JavaScript are required for this featureWhen does the limit of a multivariable function exist case of a functio of two variables;




14 Partial Derivatives Copyright Cengage Learning All Rights




Presentation On Introduction To Several Variables And Partial Derivat
Example 72 Suppose we want to describe the elevation above see level of each point on the surface of a mountain For simplicity, suppose that the mountain just looks like a cone, with the base at sea level The altitude can be represented by the function \\begin{eqnarray*} fD & \longrightarrow & {\mathbb R} \\ z & = & f(x,y), \end{eqnarray*}\ associating to each point in theA level curve can be drawn for function of two variable ,for function of three variable we have level surface A level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of fA function of three variables is a hypersurface drawn in 4 dimensions There are a few techniques one can employ to try to "picture'' a graph of three variables One is an analogue of level curves level surfaces Given



1




Level Curves
Differentiation of Functions of Several Variables Section 1 Functions of Several Variables Select Section 41 Functions of Several Variables 42 Limits and Continuity 43 Partial Derivatives 44 Tangent Planes and Linear Approximations 45 The Chain Rule 46 Directional Derivatives and the Gradient 47 Maxima/Minima Problems 48Functions of Several Variables (71) Part 2 1 Level Curves De nition 11 Level curves of a function of two variables The level curves of a function f of two variables are the curves with equations f(x;y) = k, where k is a constant in the range of f A level curve f(x;y) = k is the set of all points in the domain of f at which f takes on aGraphs, Level Curves, and Contours of Functions of Two Variables There are two standard ways to picture the values of a function f(x;y) One is to draw and label curves in the domain on which f has a constant value The other is to sketch the surface z = f(x;y) in space De nition 6 (Level Curve, Graph, Surface)




Week 1 Functions Of Several Variables




Some Examples Of Graphs Used In The Problems A Level Curves Of A Download Scientific Diagram
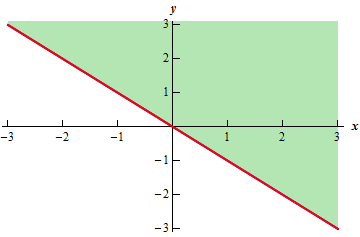
The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any number So the equations of the level curves are \(f\left( {x,y} \right) = k\) Note that sometimes the equation will be in the form \(f\left( {x,y,z} \right) = 0\) and in these cases the equations of the level curves are \(f\left( {x,y,k} \right) = 0\)The level curves in this case are just going to be lines So, for instance, if we take the level curve at z equals 0, then we have just the equation 2x plus y equals 0 And so that has interceptso we're looking atso 0 equals 2x plus y, so that's just y equals minus 2x So that's this level curve That's the level curve at z equals 0By the use of level curves we can represent these graphs in two dimensions Definition If z (x, y) is a function of two variables x and y, then the curve in an (x, y) coordinate system with points such that the x and y coordinate satisfy the equation z (x, y) = k, is called the level curve with a (function) value equal to k




Introduction To Functions Of Several Variables Ppt Download



Calculus Iii Functions Of Several Variables
141 Functions of Several Variables In singlevariable calculus we were concerned with functions that map the real numbers R to R, sometimes called "real functions of one variable'', meaning the "input'' is a single real number and the "output'' is likewise a single real number In the last chapter we considered functions taking a real number1 Consider the function f ( z) = z 2 Prove that level curves of R e ( f ( z)) and I m ( f ( z)) at z = 1 2 i are orthogonal to each other I am not sure how to apply level curves or contour lines for complex variables As far as real variables go, I am aware that for a function like f ( x, y) = x 2 y 2, the level curves are the circlesA function of two variables is a surface drawn in 3 dimensions;




4hp2d6 V Ivgnm




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



2



1



Graphs Of Functions Of Two Variables



7 Points Below Are Four Contour Diagrams Each Giving Level Curves Of A Function Of Two Variables Click On An Image To Enlarge It A B C D Course Hero




Introduction To Functions Of Several Variables



Sin X Y Sin X 2 Y 2 Images To Visualizing Functions Of Two Variables Geogebra



Draw Level Curves For Functions Of Two Variables In C C Helper
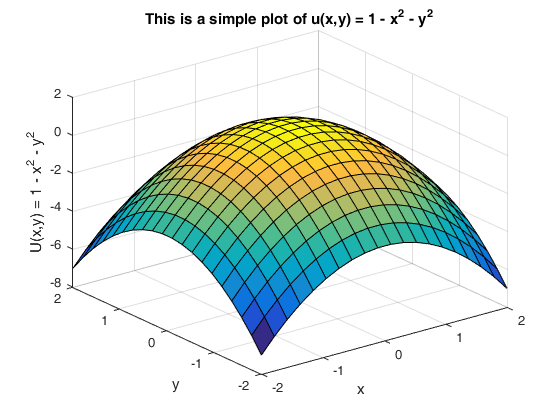



Howtoplotfunctiontwovariables



Functions Of Several Variables



Www Usna Edu Users Oceano Raylee Sm223 Ch14 1 Stewart 16 Pdf




Calculus Iii Functions Of Several Variables




Sketchthe K9 Level Curve Of T See How To Solve It At Qanda




Level Sets Math Insight




Level Curves




Functions Of Two Variables Graph Of A Function



Functions Of Two Variables Lessons Blendspace



13 1 Functions Of Several Variables Mathematics Libretexts




Level Set Wikipedia




1 Let The Function Of Two Variables Be Given As A Chegg Com



Function Of Several Variables Several Level Curves Geogebra




Vii Let Zf Xy Dfracx24 Y2 Be See How To Solve It At Qanda




In Calculus I And Ii We Worked With Functions Chegg Com




Chapter 14 Partial Derivatives Chapter 14 Partial Derivatives Ppt Download




How To Draw A Contour Map Calculus Maping Resources
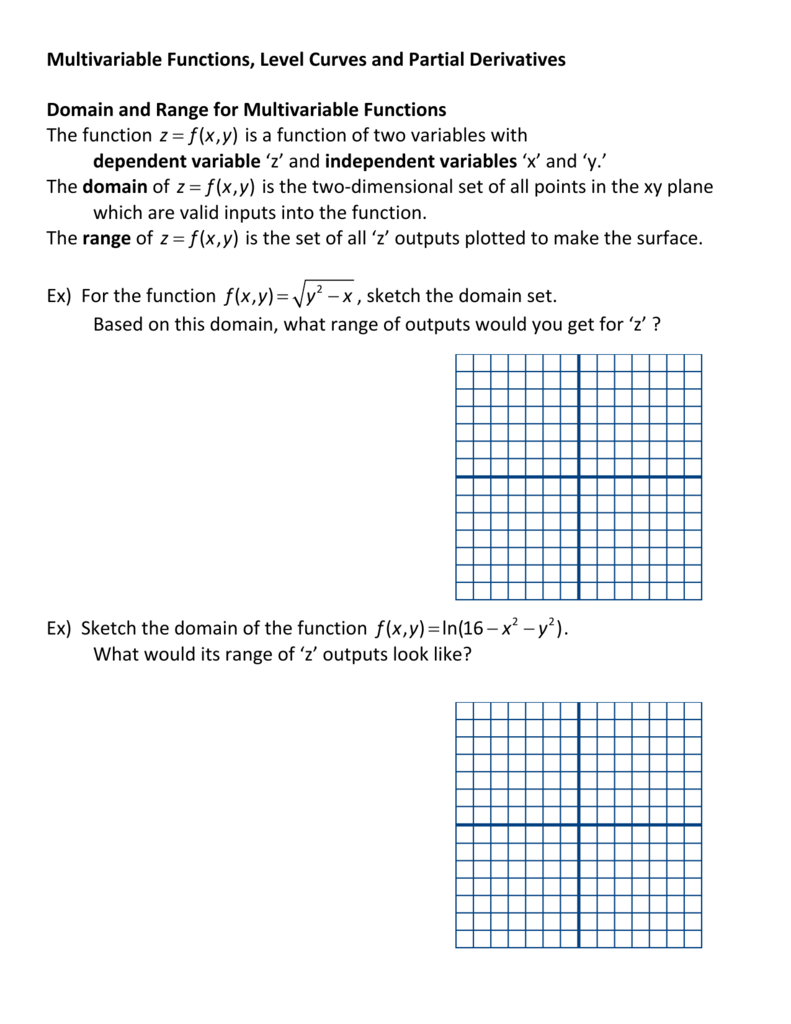



Multivariable Functions Level Curves And Partial Derivatives




13 1 Day 2 Level Curves Level Curves One Way To Visualize A Function Of Two Variables Is To Use A Scalar Field In Which The Scalar Z F X Y Is Assigned




Level Sets Math Insight



Http Diposit Ub Edu Dspace Bitstream 2445 1 Student E2 80 99s autonomous learning and tools for teachers by means of the use of geogebra 28 C3 81lvarez et al 18 29 Pdf



Http Mathcs Holycross Edu Groberts Courses Ma241 Classroom Ch11 Functions Pdf



Level Sets Math Insight




14 Partial Derivatives Partial Derivatives So Far We




Lecture Notes Chapter 1 1 Part2 Contourlines Level Curves And 3d Graphs Pdf




Calculus Iii Functions Of Several Variables
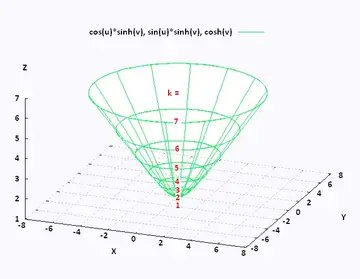



Mathematics Calculus Iii
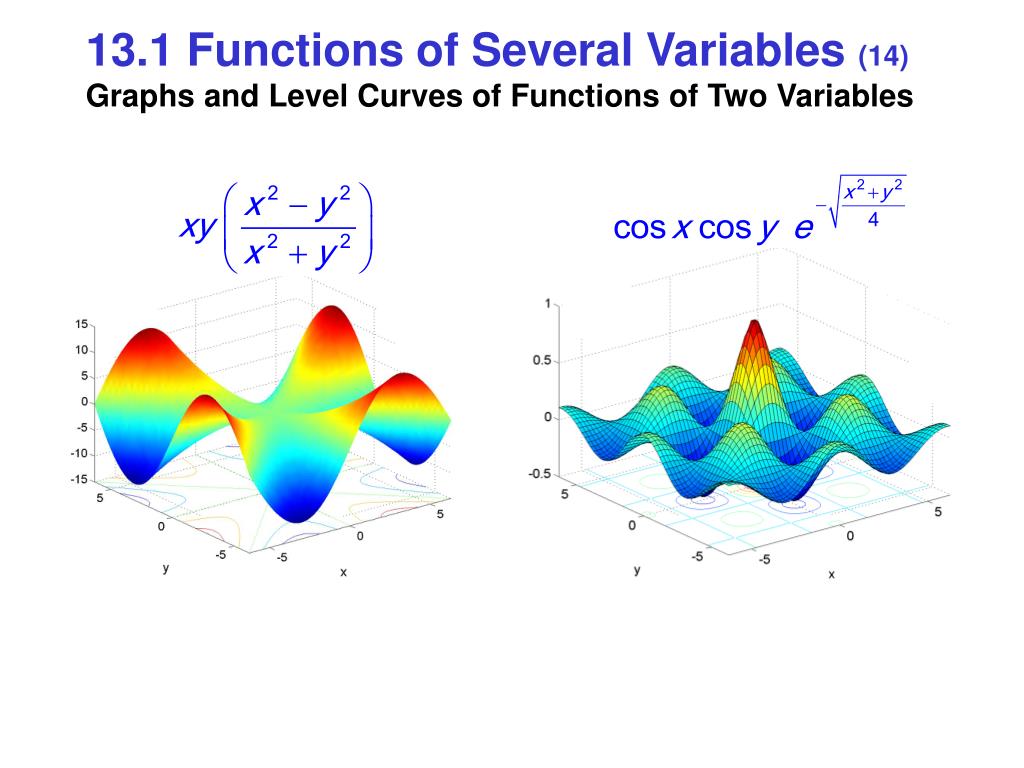



Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id
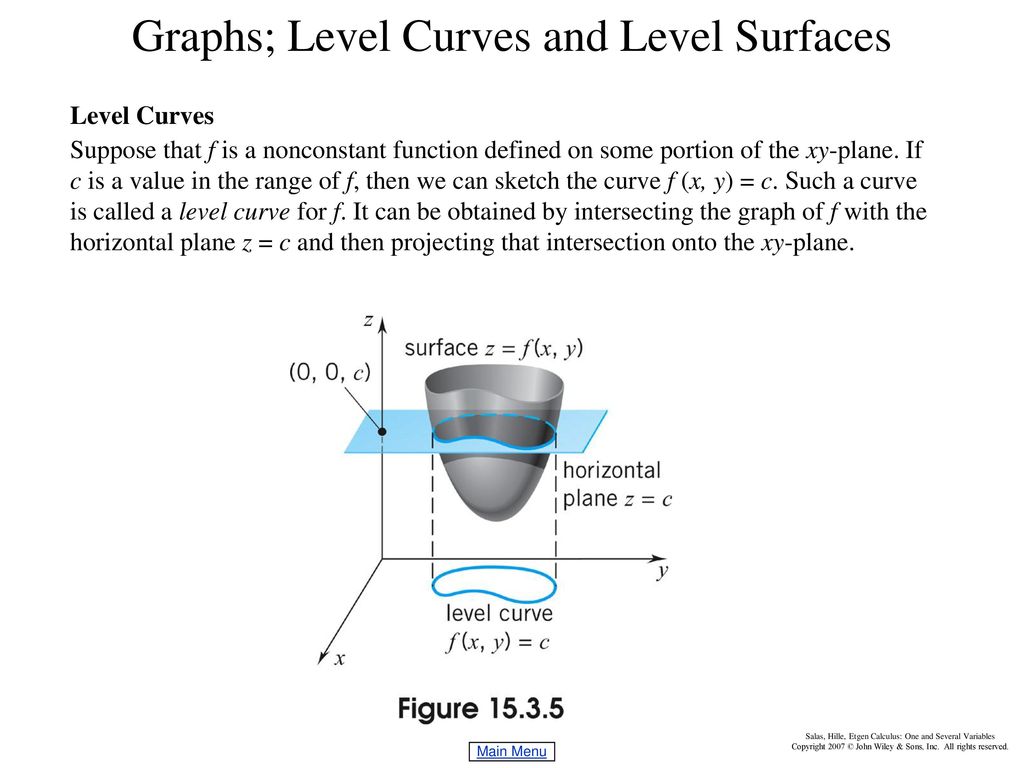



Chapter 15 Functions Of Several Variables Ppt Download




Level Curves



Http Www Mast Queensu Ca Math121 Notes Notes18 4up Pdf




Functions Of Two Variables Graph Of A Function
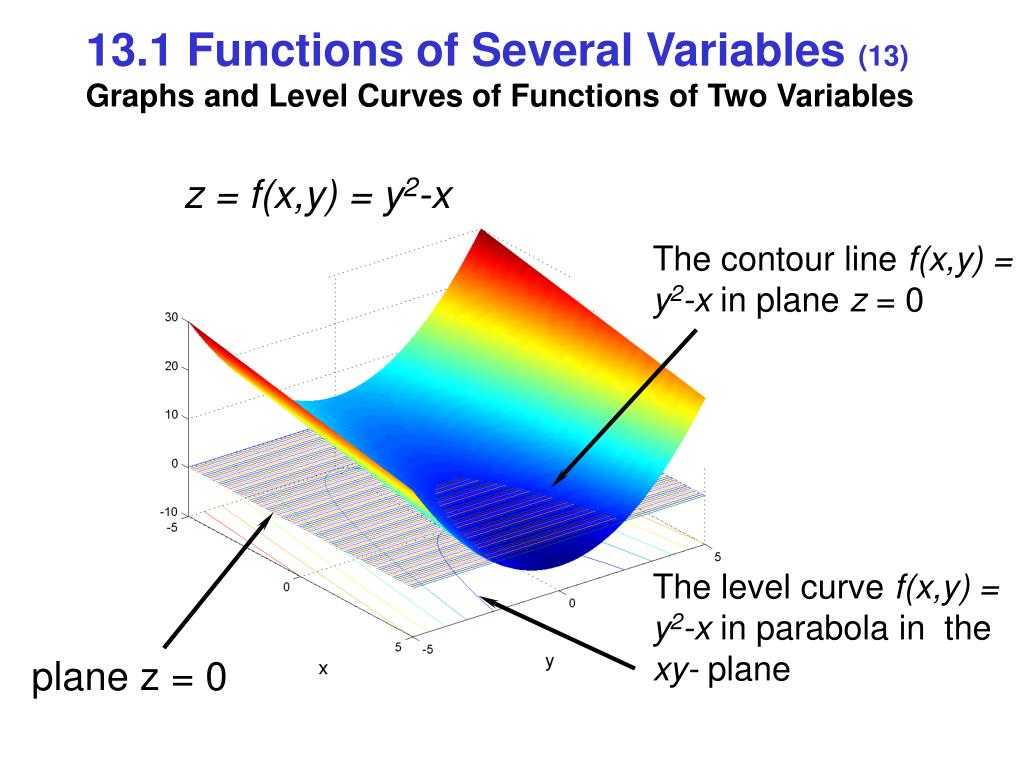



Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id




13 1 Functions Of Several Variables Mathematics Libretexts




13 1 Functions Of Several Variables Mathematics Libretexts
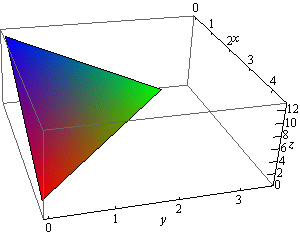



Calculus Iii Functions Of Several Variables




3 Points Writing Prompt 1 Typed 100 0 Words In Chegg Com



Www Usna Edu Users Oceano Raylee Sm223 Ch14 1 Stewart 16 Pdf



12 5 Functions Of Three Variables



The Gradient And Directional Derivative




Level Curves




Calculus Iii Functions Of Several Variables




Partial Derivatives Calculus For Engineers Iii Assignment Mat 267 Docsity




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
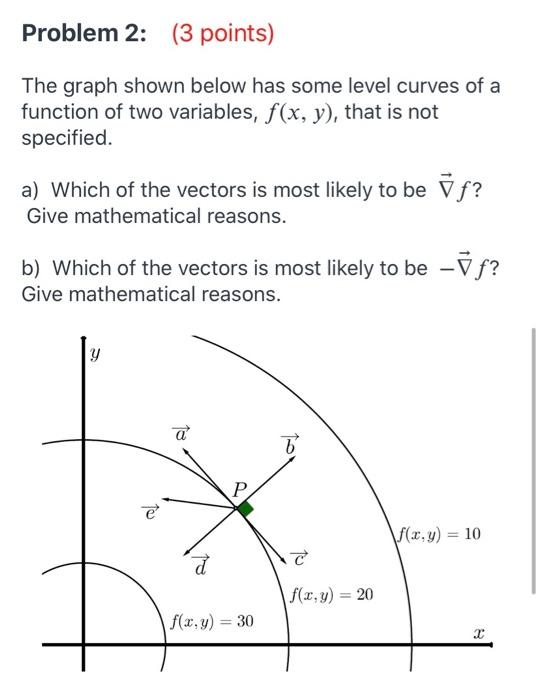



Problem 2 3 Points The Graph Shown Below Has Some Chegg Com




14 Partial Derivatives Copyright Cengage Learning All Rights




13 1 Functions Of Several Variables Introduction To Functions Of Several Variables Objectives Functions Of Several Variables Pdf Free Download




16 1 Functions Of Several Variables




Multivariable Functions And Their Level Curves Dave4math




Math146 Co3 Lec 2 Continuous Function Function Mathematics




Calculus Iii Functions Of Several Variables
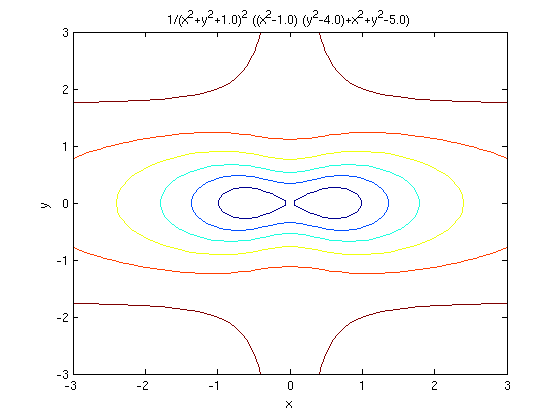



Visualizing Functions Of Several Variables And Surfaces
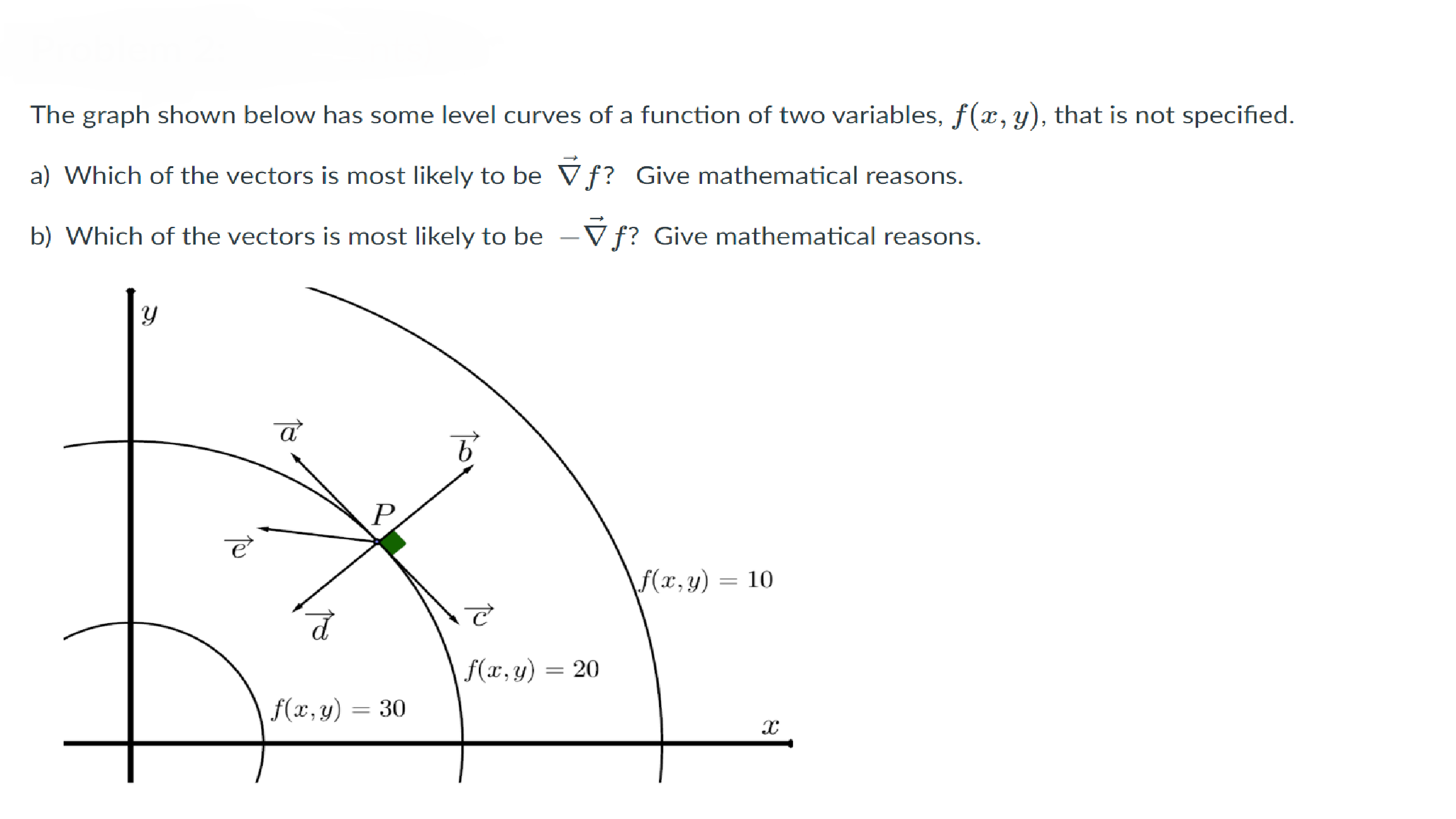



The Graph Shown Below Has Some Level Curves Of A Chegg Com



Www Usna Edu Users Oceano Raylee Sm223 Ch14 1 Stewart 16 Pdf



Www Math Uci Edu Remote Teaching Lecture Notes Of Hamed Math 2d lecture notes Lecture note 14 1 Pdf
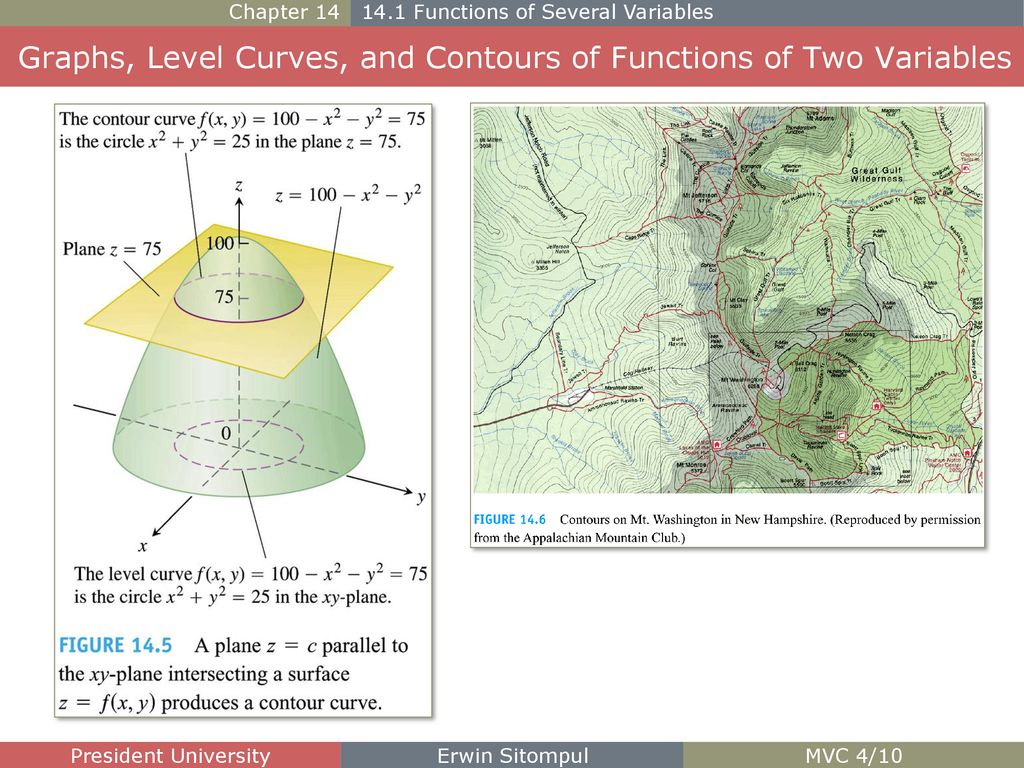



Chapter 14 Partial Derivatives Chapter 14 Partial Derivatives Ppt Download



Labware Ma35 Multivariable Calculus Two Variable Calculus
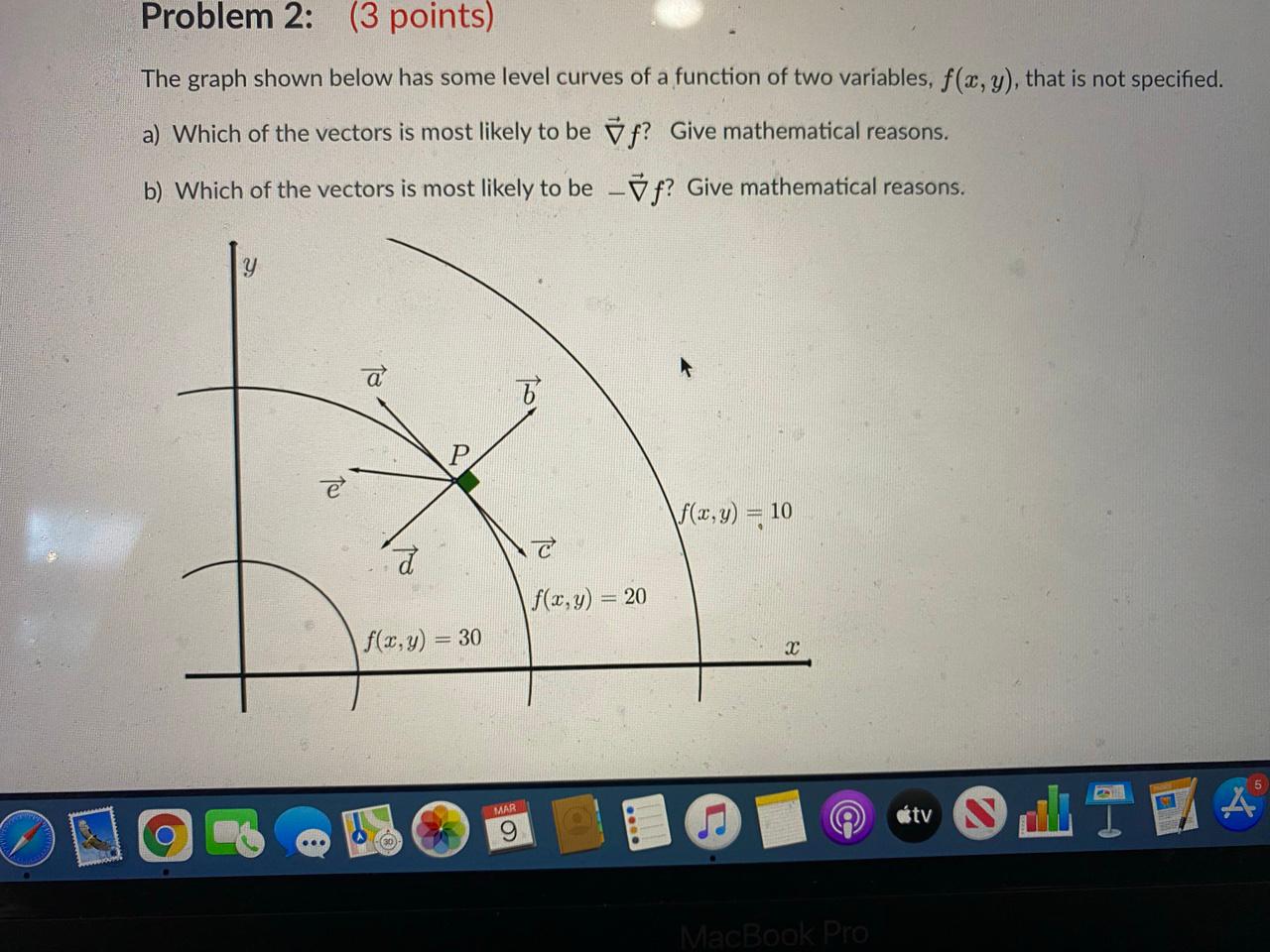



Solved Problem 2 3 Points The Graph Shown Below Has So Chegg Com
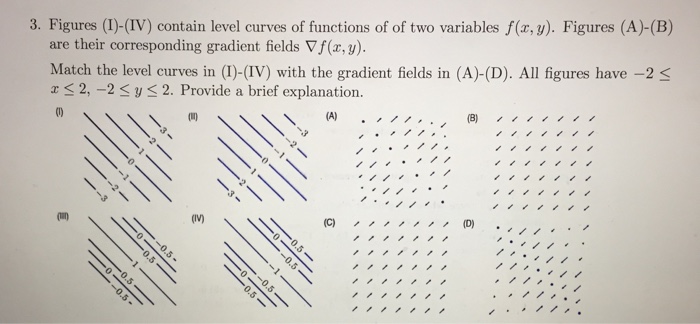



Figures I Iv Contain Level Curves Of Functions Of Chegg Com




How Do You Sketch Level Curves Of Multivariable Functions Youtube



Procedure For Computation Of The Goodness Of Fit Indicators Two Download Scientific Diagram




Chapter 14 Partial Derivatives Chapter 14 Partial Derivatives Ppt Download



8 Calculus Of Several Variables Functions Of Several Variables Ppt Download




8 Calculus Of Several Variables U Functions Of




Level Set Wikipedia




Level Sets Math Insight
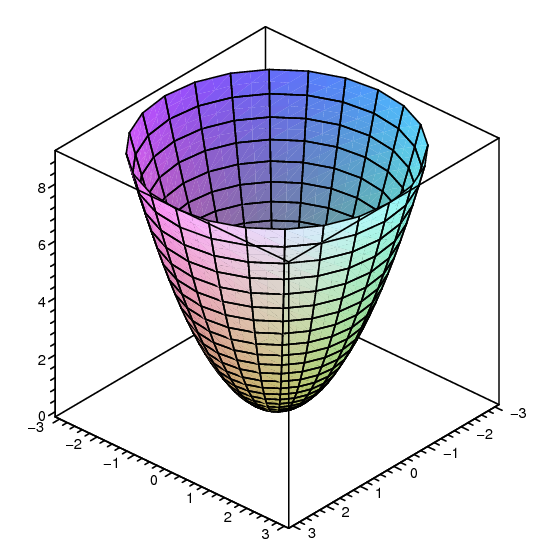



16 1 Functions Of Several Variables



Http Math Oregonstate Edu Garity 254h Winter13 Notes 10 Graphs Levelcurves Pdf




Level Curves Of Functions Of Two Variables Youtube



0 件のコメント:
コメントを投稿